The Si(111) surface consists of double layers of atoms singly bonded to each other (FIg. 1.10b). In each double layer, a mesh of tetrahedral bonds connects the atoms in a threefold symmetry (Fig. 1.10a). The (111) plane is formed by breaking the perpendicular bonds between double layers. Once these bonds are broken, the first two atomic layers and the fourth atomic layer are exposed to the surface (Fig. 1.10a). Since these dangling bonds are highly energetic (cf. Fig. 1.10a), surface atoms rearrange at room temperature to minimize the total surface energy.
A cleaved Si(111) surface has been shown to be \(2\times 1\) reconstructed (Fig. 1.10b). This reconstruction occurs by rearrangement of the 6-atom rings (Fig. 1.10a) into rings of five or seven atoms. The total number of atoms remains constant. However, the formation of \(\pi-\)bonds among the rings lowers the net free energy of the surface. The \(2\times 1\) reconstruction is thus attained to minimize surface free energy.
Figure 1.10: Model of the Ideal Si(111)\(1\times 1\) Surface. a) A top view of the silicon surface. b) Side view of the silicon surface layers shows the second double-layer (in the bulk) with one of the two atoms hidden from the surface by a perpendicular bond between double-layer planes. |
Annealing the \(2\times 1\) surface results in another reconstruction effort to further minimize free energy. The first evidence of this reconstruction resulted from low energy electron diffraction (LEED) experiments in which "very large-spaced structures on the (111) surface"[1] were observed on samples annealed at \(650^\circ\textrm{C}\) for a few hours after heating at \(1000^\circ\textrm{C}\) for a few minutes following ion bombardment at 150 - 500 eV. The observed \(7\times 7\) reconstruction further minimizes the surface energy by 60 meV per \(1\times 1\) unit cell[2]. The \(7\times 7\) surface reconstruction is stable at temperatures below \(830^\circ\textrm{C}\).
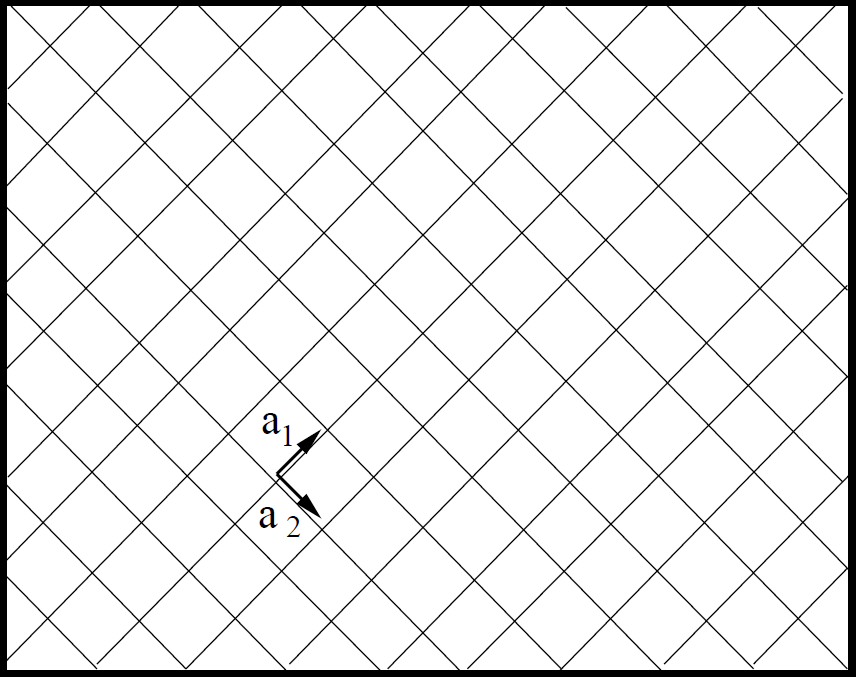
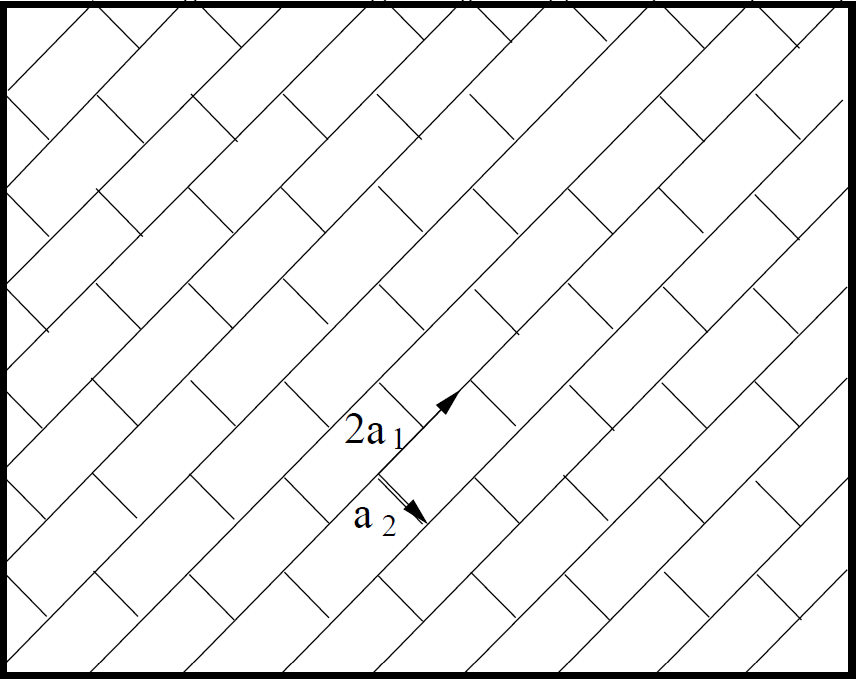
Figure 1.11: \(1\times 1\) and \(2\times 1\) Surface Schematic. a) \(1\times 1\) and b) \(2\times 1\) surface. The primitive unit cell vectors of the \(2\times 1\) reconstruction are integral magnitudes of the \(1\times 1\) unit vectors. |
Other same-integer multiples of the unit vector reconstruction have been shown to have smaller energy changes than the \(7\times 7\) case.1 Therefore, the \(7\times 7\) reconstruction is more energetically favorable.
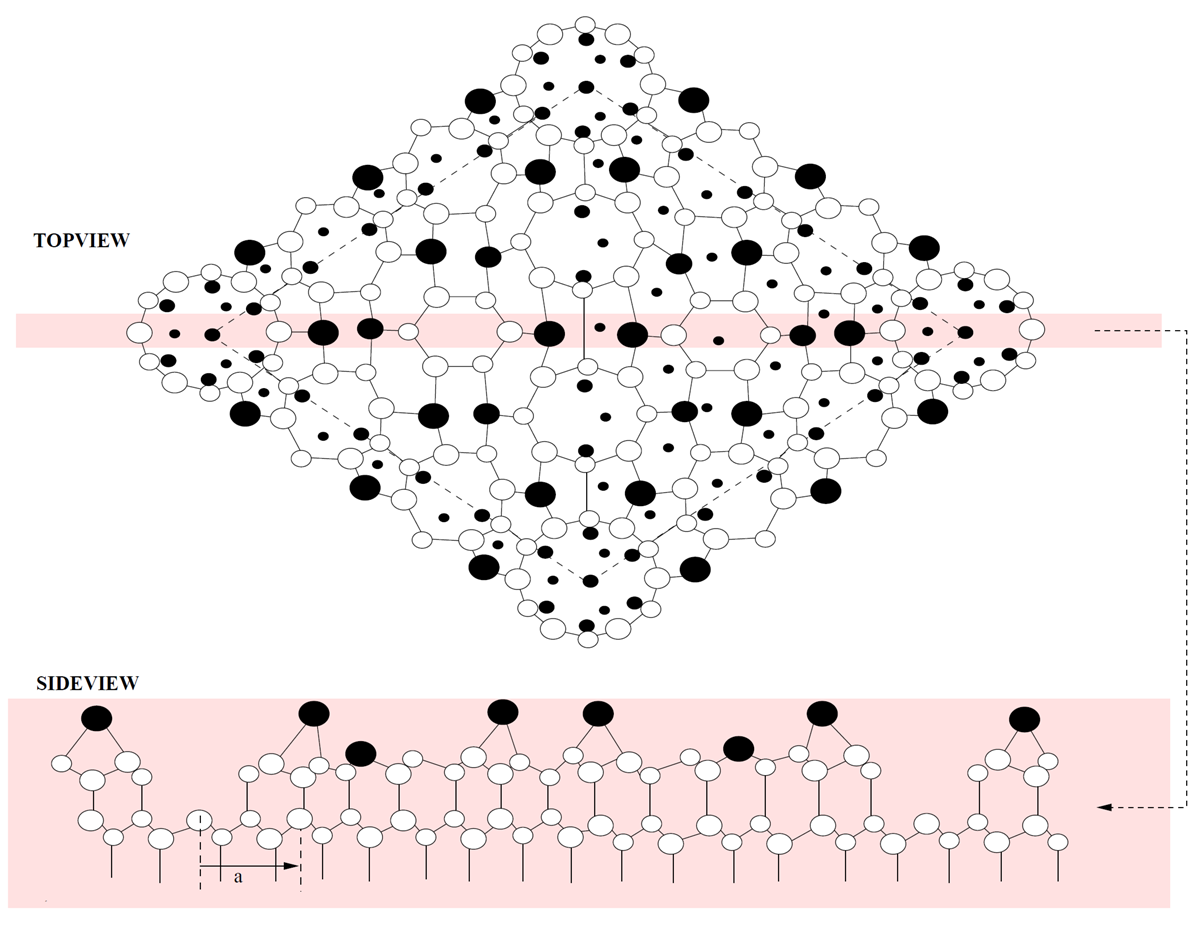
Figure 1.12a shows the top view of the reconstructed \(7\times 7\) unit cell. The large atoms form the topmost surface layer. The cross-sectional view (Fig. 1.12b) shows the \(7\times 7\) unit cell extending into the first few layers of the substrate surface. Hence, the dimensional spacing of the outermost surface layers differ dramatically from the bulk lattice spacing. The actual planar variations can not be calculated numerically2
Figure 1.12: \(7\times 7\) Reconstructed Superstructure. a) A planar view of the \(7\times 7\) surface superstructure. Dashed lines represent the perimeter of the unit cell. Large solid atoms are the topmost surface adatoms (twelve in each unit cell). b) A cross-sectional view of the \(7\times 7\) superstructure. Notice the dramatic difference between "surface" layers with respect to the bulk crystal lattice. |
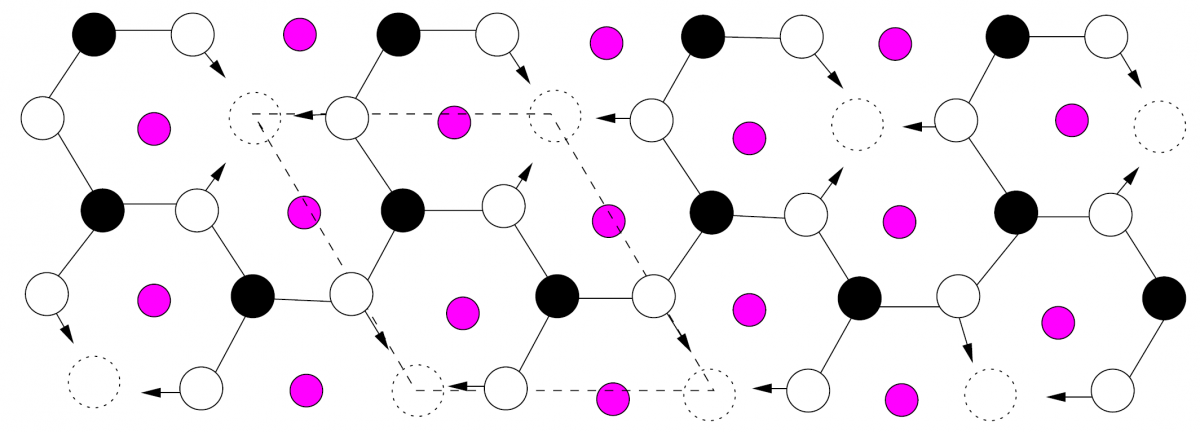
The most common reconstruction of Si(111) is \(\sqrt{3}\times \sqrt{3}\). Originally[4], the \(\sqrt{3}\times \sqrt{3}\) reconstruction of the Si(111) surface was considered a surface vacancy phenomenon. This reconstructed vacancy surface (Fig. 1.13) was found to be very unstable, remaining at most for a few days. By filling in these vacancies with metallic atoms (e.g. group III) the \(\sqrt{3}\times \sqrt{3}\) reconstruction remained very stable. In original solid-metal-mediated experiments[5] 0.3 ML of Al was initially deposited to induce and maintain a \(\sqrt{3}\times \sqrt{3}\) surface reconstruction of Si(111) substrates.
|
Figure 1.13: The Unstable Vacancy Model of the \(\sqrt{3}\times \sqrt{3}\) Surface. Dashed lines form the perimeter of the primitive surface lattice. Dashed circles are vacancy locations that may be occupied by a monolayer of adatoms for stability. |
References
- , “Structure and adsorption of clean surfaces of germanium and silicon”, J. Chem. Phys., vol. 30, 1959.
- , “Ab initio theory of the Si(111)-(7x7) surface reconstruction: a challenge for massively parallel computation”, Phys. Rev. Lett., vol. 68, no. 9, 1992.
- , “Ab initio total-energy calculation for extremely large systems: application to the Takayanagi reconstruction of Si(111)”, Phys. Rev. Lett., vol. 68, no. 9, 1992.
- , “Observation and structural determination of (√3×√3)R30° reconstruction of the Si(111) Surface”, Phys. Rev. Lett., vol. 62, 1989.
- , “Epitaxial Growth of Si(111) at Buried Interfaces Using Solid-Metal Mediated Molecular Beam Epitaxy”, in 1996 MRS Spring Meeting, San Francisco, CA, 1996.
- 1. Numerical values of 10.7656, 29.205, and 56.509 meV for the \(3\times 3\), \(5\times 5\) and \(7\times 7\) cases, respectively, are provided in the literature[3]. The surface energies saturate near the \(7\times 7\) configuration and so larger multiples may be energetically unfavorable.
- 2. Reference [2] provides numerical calculations of atomic spacing in the \(7\times 7\) superstructure.