Week of November 14, 2021

As I noted in my previous blog entry, Electron Shell-Filling Made Easy, I want to discuss how Coulomb's Law is geometry -- a concept that is especially useful in certain circumstances when you want to simplify  calculations or develop a better intuition about interactions with electric fields. For the purpose of this discussion we'll confine ourselves to an interest in systems of electrons in free space. Why? Because the amount of charge every electron possesses is identically equal in magnitude, and free space is a uniform environment in which to play with physics ideas -- like a coder's sandbox.

The aim here is to impress upon you the idea that electric force and the stored energy associated with the electric force are very much determined by the geometric arrangement of electrons in a system. I have a kind of personal bias in this matter since geometry is very much at the heart of the entire body of work I've developed concerning connections between classical physics and electrons in atomic structure. More specifically, the unique geometric changes that occur in systems of electrons (such as atoms!) is the literal heart of the discovery I made concerning the entire periodic table of elements. Though I say this is a personal bias, it is a very much a physics-supported bias and deserves far more attention than the subject typically receives in physics courses at all levels  -- introductory, intermediate, and advanced.

Let's get started.

The Physical Quantities

Coulomb's Law is an equation that relates the electric force between two sources of charge and the material property of the space between them. Associated with this electric force is a quantity of electrostatic potential energy between two point particles having charges q_i and q_j separated by a distance r_ij,

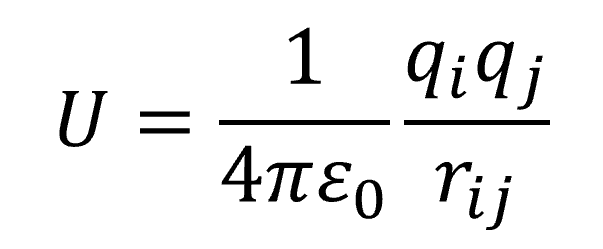
with ɛ₀ the permittivity of free space between them. The physical quantities involved in this equation are the two magnitudes of charge, the energy, U, and ɛ_0. Since we're only concerned with electron charges, we can set both of these charges to e, the elementary charge that has the value of 1.602 × 10^-19 Coulombs. For most people, this value has very little meaning because the number is extremely small compared to anything most people will every encounter in their everyday lives. Worse, the value of ɛ₀ is 8.85418782 × 10^-12 m^-3 kg^-1 s⁴ A². Not only is this also an extremely small number that most people would never encounter, but the units likely mean nothing to most people either. I won't bother explaining the abbreviations at this point, because that's not the aim of this blog entry. In fact, what we really want to do it get rid of these numbers so we won't have to think or worry about them at all. So, making this equation simpler will be a great thing.

To make this equation very simple, we can apply a great piece of knowledge that scientists have confirmed by measurement and theory for over a century: the values of e and ɛ₀  never change. So why would we want to waste our time dragging these tiny numbers with strange units around in our calculations of the equation? This may not be such a big deal to you if you have a calculator on-hand, but what if I told you that every calculation you do will require to repeat an evaluation of this equation say 100 or 1,000 times? This would not only be tedious, but it's entirely unnecessary. So let's not do it. In fact, let's just set these values to 1 and only worry about it if anyone asks us about our final calculated results.

At this point then, we've chosen to evaluate Coulomb's law for electrostatic potential energy in the form

where we've set all the physical quantities to 1. That is, qi = qj = e = 1 and ɛ₀ = 1.

We're justified in doing this because all electrons have the same elementary charge and the properties of free space are unchanged. In fact, the only thing that may change is the distance between every pair of electrons, r_ij.

The Geometric Quantities

In addition to the physical quantities that appear in Coulomb's law is the inherent geometric quantity 4π. This appears in the form of the three-dimensional angular space around one of the two charged particles, q_i or q_j. The reason 4π appears in the equation -- in fact, it appears in many physics equations -- is because in order to evaluate the total electrostatic potential energy in the spherical volume surrounding the test charge, qi, we must account for the entire volume. The total solid angle that accounts for this volume is 4π steradians. Why a sphere? Because the strength of the electric field on the surface of any sphere of a given radius from a point charge, like qi, is the same. I mention this mostly to emphasize the inherent presence of geometric quantities in Coulomb's law, but now that we know the solid angle of a sphere is always 4π, let's set this to 1 also. This leaves Coulomb's law in the form

where the only remaining quantity to evaluate is r_ij for every pair of electrons in a system. Because r_ij is a quantity that can be measured, it is considered a physical quantity, but since here we are working with the Thomson Problem, we can simply reference the magnitude of r_ij to the size of the sphere. This is why the Thomson Problem is solved for electrons distributed on a "unit sphere". It's a sphere of radius 1. We don't care if this is 1 meter, 1 mile, 1 parsec, or 1 femtometer. It doesn't matter. This is because the size of the Thomson sphere doesn't matter. It doesn't affect the solution which is the lowest-energy configuration of N electrons on the surface of the sphere. This fact is the subject of the next blog entry -- Size Doesn't Matter.

Therefore, Coulomb's Law is just geometry.

Before we leave it at that, let's drive home the point of why we want to do this. I want to discuss this as a kind of personal conveyance of experience and motivation for anyone who doesn't yet grasp the exciting desire to have simplified a physics equations that we'll use over and over again. So let's dive into what may well be thought of as a 'calculation drag." It's also 2021, so here's a little opportunity for many of you to learn about online technologies like Google calculator to make your life easier.

The Calculation Drag

Many decades ago the ability to perform calculations was restricted to hand-written equations and so-called long-form mathematical operations on a blackboard or pieces of relatively expensive paper. Among other reasons, I believe the tedium and time-consuming nature of performing complicated calculations in those times largely fueled the need to simplify the mathematical expressions much moreso than scientists and engineers are inclined to do today. After all, most scientists and engineers have the computational tools at our disposal today that we can afford to ignore any simplifications whatsoever and just brute force our way through calculations. Even the Google Calculator panders to this brute force approach. Try it. Go ahead and google the following:

(elementary charge)^2 / (4*pi)

and it'll return

2.04272976 × 10^-39 s² A²

You may not like the units of seconds square amperes square, so just ask Google to give it to you in Coulombs square:

(elementary charge)^2 / (4*pi) in Coulombs^2

and it'll return

2.04272976 × 10^-39 coulombs^2.

That's because Google knows the value of π and it knows the value and units of the elementary charge, e.

What else can you learn from this simple activity? If you're quick-enough you would have already compared the numerical value of the two returned answers and know that 1 second * Ampere = 1 Coulomb, but don't worry. If you didn't see it just ask Google to tell you the relationship. Search for

1 second*ampere in Coulombs

and it'll return

Most numerical energy solutions of the Thomson problem are reported in implied units of inverse distance (1/r_ij). Hence, the numerical solution for the N=2 Thomson problem is simply 0.5 because the two electrons are separated by two radius lengths, or 2 units of distance. The solution for N=3 is the result of adding the inverse distances of the side of an equilateral triangle, and so on. See the table of numerical Thomson Problem solutions on Wikipedia for an example.

Here we discussed how the motivation to simplify Coulomb's law revealed that electrostatic energy is intimately related to the geometric properties of a collection of charged particles. This is at the very heart of the discovery I made connecting the Thomson Problem to the periodic table of elements. The varying geometric symmetry differences between neighboring Thomson Problem solutions, in fact, is what led me to believe that there must be a connection that no one had seen before. I recall thinking "the symmetry differences are there, but why hasn't anyone seen the connection?!" I'll reserve my thoughts on this for yet another future blog entry.

Next Week

Not only do we use the geometric form of Coulomb's law to simplify our physics calculations in the Thomson problem, but we also choose the sphere to be unit in size so we don't need to worry about the units whatsoever. In fact, the size of the Thomson sphere is completely irrelevant. The sphere can be any size. It could be the size of the universe, the size of the sun, the size of the moon, the size of your head, or the size of your phone, or the size of an atom. The geometric symmetry of every Thomson problem solution never changes despite the size of the Thomson sphere.

And that is the subject of next weeks blog entry, Size Doesn't Matter.