It's not that achieving 300 reads on one of my published papers today is a huge deal, but it is a way for me to briefly post some remarks here about something that bothered me enough during my doctoral research program that helped lead me to constructive thinking about the problem. The problem at hand is called the Thomson Problem. it's a great three-dimensional physics problem whose objective is to find the geometric configuration of electrons constrained the surface of a mathematical sphere of unit radius. You can find a freely-available copy of the paper I want to discuss here on arxiv: Discrete transformations in the Thomson problem.

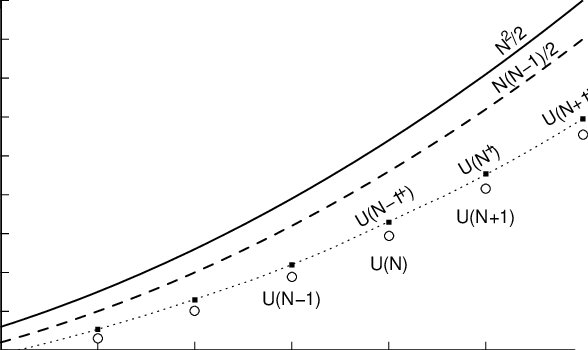
In particular, I want to briefly discuss the plot of electrostatic potential energy solutions for each N-electron system. In the figure below, the energy solutions of the Thomson Problem are the lowest distribution of open circles with data points labeled $U(N-1)$, $U(N)$, $U(N+1)$, and so forth. The two distributions, indicated by smooth, continuous function $N^2/2$ for a spherical metallic shell, and $N(N-1)/2$ is the energy of a purely random distribution of $N$ electrons on the sphere. These represent upper limits to the solutions of the Thomson problem.

In the figure are also solid black circles. These represent my starting upper limit to the solutions of the Thomson Problem and represent any $N$ electron system with $N-1$ electrons on the surface of the sphere and one electron at the center of the sphere. It's that little gap between these solid circles and the open circles is the amount of energy standing between mathematicians and exact solutions of the Thomson problem. After all, the Thomson Problem remains an unsolved mathematical problem, appearing on Steve Smale's list of challenge problems for the 21st century.

Now, many other researchers have focused on the possible existence of a smooth function connecting all the exact solutions of the Thomson problem. I'll not get into those here, but I want you to think about what physically realistic processes would be involved if such a smooth, continuous or piecewise-continuous function existed. That's what is represented in the next figure below.

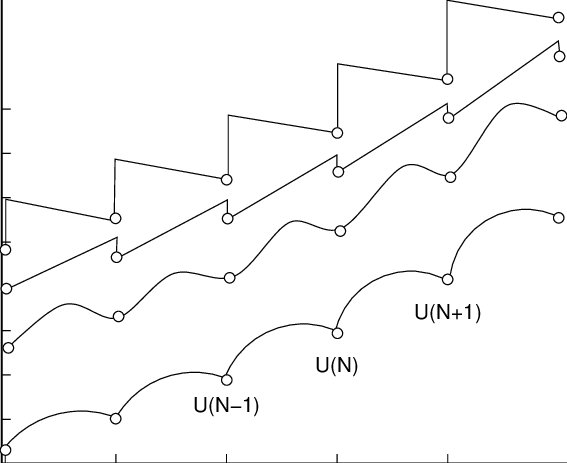
Here's the original caption of this figure in the paper (note: $q_0$ represents my electron charge at the center of the sphere):

" A few possible continuous fit functions to minimized energy solutions of the Thomson Problem. a) $q_0$ is introduced abruptly to each $N$-charge solution, and the energy is gradually minimized to $U (N + 1)$. b) $q_0$ forms gradually at the origin, and the total energy is minimized to $U (N + 1)$. c) Energy minima are obtained with a smooth, periodic function having minima at integer values of $N$ . d) Energy solutions are obtained with a piecewise-continuous function with minima at integer $N$ values."

There may be other possible processes of moving electrons around in the system than those I suggested in the paper that may yield a smooth, continuous or piecewise-continuous function, but here I wanted to give some examples to illustrate the point that there are no continuously divisible charged particles that we know of in the universe. So, if we were to string a function smoothly through all the data point solutions like the first figure with something like $N^2/2$, we are no longer discussing a physically realistic system. Furthermore, each data point represents a minimum of electrostatic energy, so any smooth function must have a local minimum at each of these data points -- another reason why a simple smooth function is unrealistic.

Perhaps the physical processes involved in the connecting smooth functions between solutions is something that occurs in the mathematical framework of quantum mechanics. The general solution to the Thomson problem may very well be inspired by the quantum mechanical description of atomic structure -- after all, as a reader of my blog, you know these solutions are intimately connected to atoms appearing throughout the periodic table of elements.

However, I wanted to convey my thinking about how others have assumed a priori that there is some simple mathematical function that strings all the solutions together that is functionally proportional to $N^2/2$. It truly bothered me enough to see that kind of work that I was led to think about that's really at play behind the physical process of adding or removing an electron from the system that might eventually lead us to a general solution of the Thomson Problem.

The $q_0$ Transformation

Now, back to the transformation -- moving one electron to or from the origin of the sphere.

In the picture below, note the number of charges on the horizontal axis. There are either $N$ or $N+1$ electrons in the example system. You see three spherical examples. The lower-left picture has only three electrons ($N=4$ in this case) and the lower-right picture has four electrons ($N+1=5$ in this case).

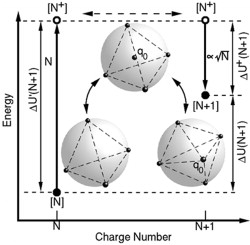
To get to the 5-electron solution of the Thomson problem, starting from the lower-left picture of 4 electrons, you could add one electron to the center of the sphere. When this happens, the geometric symmetry of the original 4 electrons does not change. They still form a regular tetrahedron with vertices on the surface of the sphere. Notably, however, this requires a change of energy in the system (generally, an increase in energy!) equal to $\Delta U'(N+1)$ as indicated on the left. If we were plot all of these transition energies for all $N$ (e.g. adding one electron to $N=10$, then $N=11$, then $N=12$ and so on), the change in energy increases linearly with respect to $N$. Therefore, if the initial solution of the Thomson problem (in the figure below, that is, for $N=4$ -- which is one of very few exact solutions, incidentally), then the solution of the upper figure with one electron of charge $q_0$ at the origin, is an exact solution as well.

Continuing the transformation to the $N=5$ electron solution, $q_0$ must move from the origin to the surface of the sphere (the lower-right figure). The energy needed to make this transition, denoted here as $\Delta U^{+}(N+1)$ is approximately proportional to $\sqrt{N}$, but it's not an exact functional dependence. In fact, I believe the $\sqrt{N}$ trend stems from the statistical nature that connects the discrete solutions of the Thomson problem with whatever smooth, general function may exist as a solution of the Thomson problem. It is, in fact, this transition energy for every $N$ electron system, that is the essence of a general solution of the Thomson problem. It isn't yet exactly known. Perhaps there is no exact solution, and perhaps this -- more philosophically -- is why there are so few exact solutions generated by quantum mechanics for atomic systems. Let that not prevent anyone from delving into a quest for the general solution, however.

Alternatively, think about the reverse process depicted in the picture. Start with the 5-electron (lower-right) case, and move an electron to the center. This, I argue, is geometrically identical to the natural process of ionization. That is, a single electron is removed from a 5-electron atom to a great distance where it has either no effect on the remaining 4 electrons, or it has nearly identical electrostatic effect on them. The resulting ion has a single net charge located at its origin -- it's a positive charge of one of its five protons whose charge is not balanced/negated by the ionized electron! In the figure there is a charge, $q_0$, at the origin. And, like the ionized electron, it has an identical electrostatic effect on the remaining 4 electrons at the surface of the sphere. So, geometrically the process depicted in the figure is identical to the natural process of ionization. Physically, we have yet to account for the difference in the sign of the electron charge $q_0$.

One approach to complete the physical picture of comparing these processes I offer is to consider the concept of an image charge in electrostatic systems involving excess or free electrons in a dielectric material.

The mathematical image of a negative point charge physically located inside a spherical dielectric (like an atom, by the way) has a positive charge sign and is located outside the dielectric. As the charge inside the sphere approaches the origin of the sphere, its image moves (mathematically)  to its farthest distance from the sphere (like an ionized electron!). Alternatively, as $q_0$ moves to the surface of the sphere, its image charge returns to the surface of the sphere.

How to comprehensively connect these geometric and physical constructs? That's a great question I believe gets us to the heart of the problem. In other words, how do we connect the classical electrostatic solutions of the Thomson Problem (geometry combined with Coulomb's Law) with quantum mechanical solutions of orbitals (for example) in real atoms? Perhaps the mathematical connection involves imaginary image charges and a means of flipping the sign by mathematical symmetry?