The integral form of the error function[1], $\textrm{erf}(x)$, is

$$\textrm{erf}(x) = \frac{2}{\sqrt{\pi}}\int_{0}^{x} \textrm{e}^{-z^2}dz. $$

Its series is given by,

$$\textrm{erf}(x) = \frac{2}{\sqrt{\pi}} \left( x - \frac{x^3}{1!\cdot 3} + \frac{x^5}{2!\cdot 5} - + \cdots \right).$$

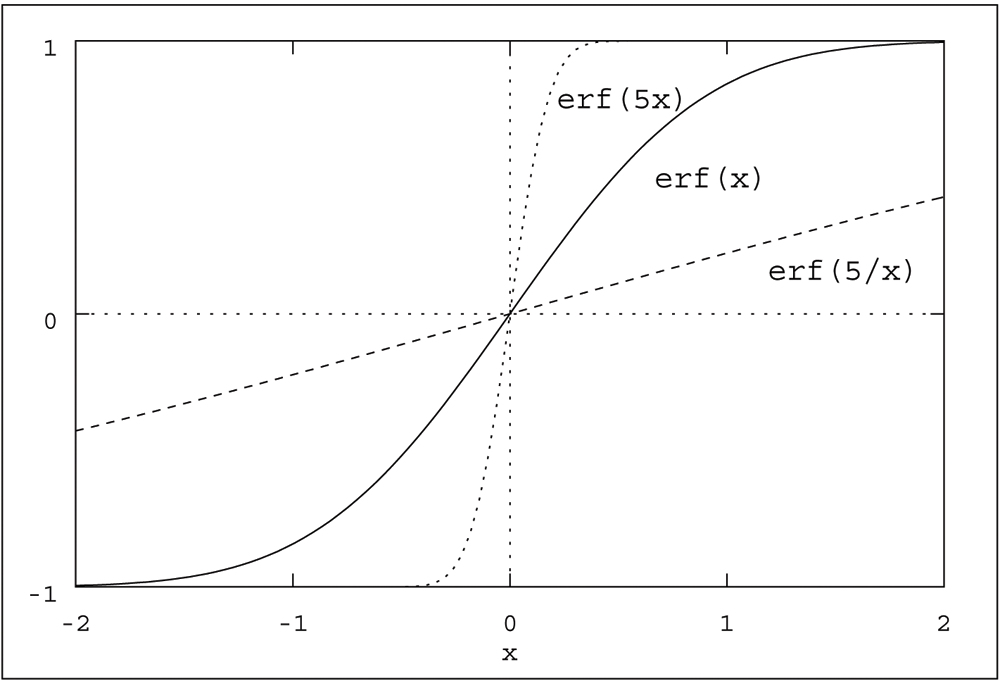
The error function is graphically represented in Figure A.2. Notice that as $x \longrightarrow \infty$, $\textrm{erf}(\infty) \longrightarrow 1$.

The complementary error function is given by definition,

$$\begin{array}{rcl}\textrm{erfc}(x) &=& 1 - \textrm{erf}(x)\\ &=& \frac{2}{\pi} \int_{x}^{\infty} \textrm{e}^{-z^2}\textrm{d}z,\end{array}$$

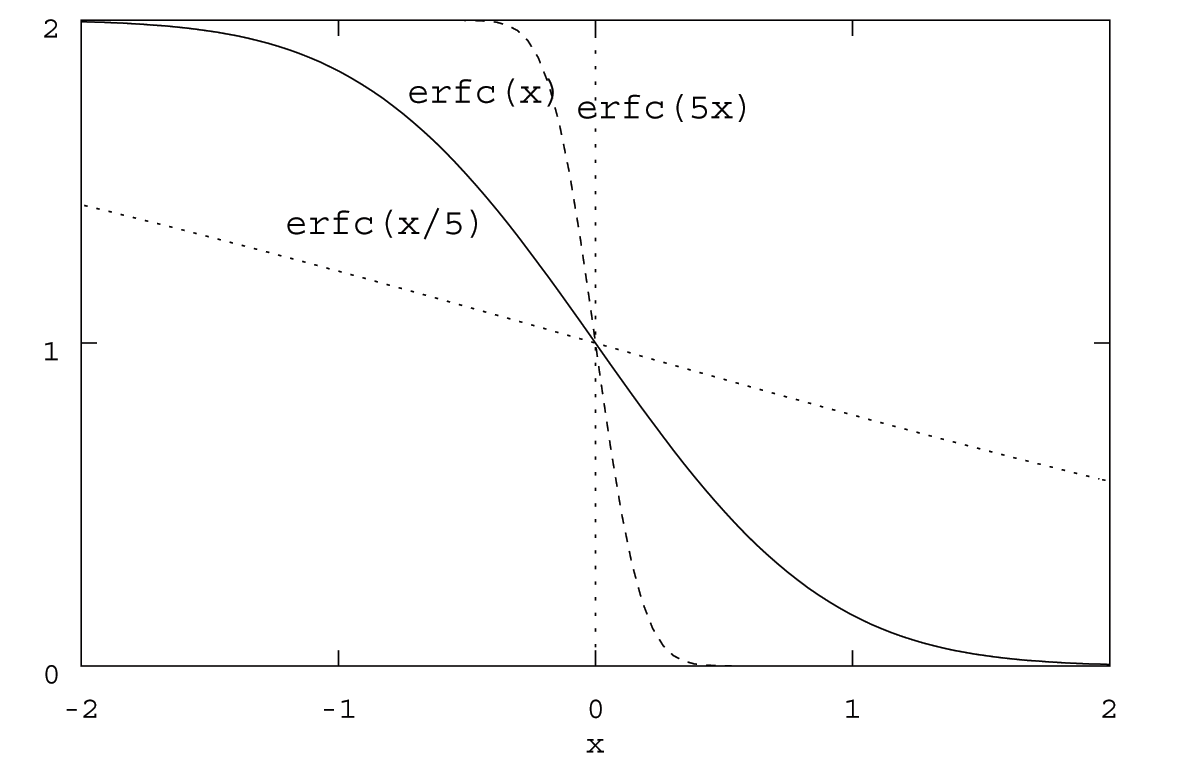
and is graphically illustrated in Figure A.3. Notice that at $x = 0$ the value of the complementary error function remains fixed for all values of the argument. This satisfies the imposed surface (boundary) conditions.

References