The familiar result of the gaussian integral
$$ I = \int_{0}^{\infty} \textrm{e}^{-x^2} dx $$
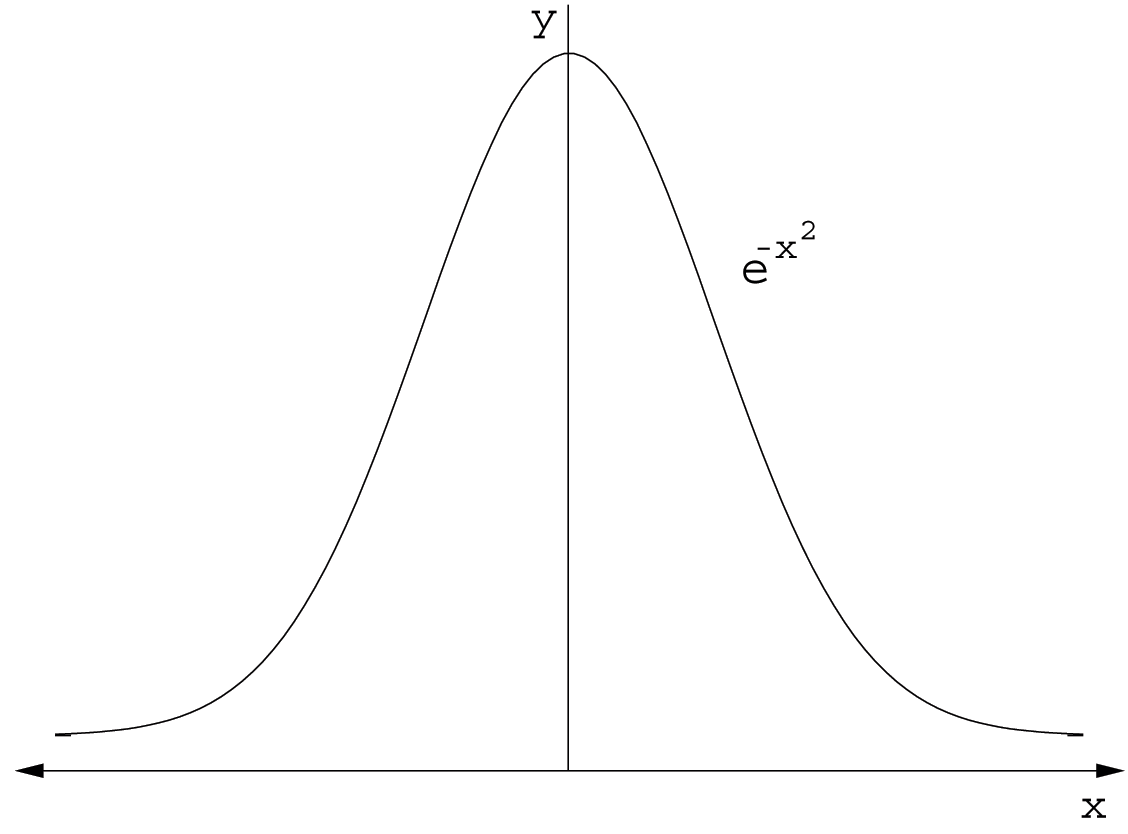
can be obtained by symmetry (Fig. A.1}) about the $y$-axis,
$$ I = \frac{1}{2} \int_{-\infty}^{\infty} \textrm{e}^{-x^2} dx.$$
| Figure A.1. Symmetry of the Gaussian Function, $\textrm{e}^{-x^2}$. |
Square the integral and convert it to polar coordinates,
$$\begin{array}{rcl}I^2 &=& \frac{1}{4} \int \int_{-\infty}^{\infty} \textrm{e}^{-x^2} \textrm{e}^{-y^2} \textrm{d}x \textrm{d}y\\&=& \frac{1}{4} \int_0^{2\pi} \int_0^{\infty} \textrm{e}^{-r^2} r \textrm{d}r \textrm{d}\theta\\&=& \frac{1}{4} 2\pi \cdot \frac{1}{2}\end{array}$$
where $\textrm{d}x\textrm{d}y = r \textrm{d}r \textrm{d}\theta$.
Finally,
$$I = \frac{\sqrt{\pi}}{2}.$$